Bayesian Optimization

What is Bayesian Optimization?

One of the oldest and most widely used instantiations of sequential model-based search is Bayesian optimization. There are a number of great tutorials and review articles on Bayesian optimization, and we won’t repeat them here:

Most instances of Bayesian optimization work by modelling the objective as function \(f(\mathbf{x})\), where \(\mathbf{x}\) is a configuration from the search space. Given such a probabilistic surrogate model, we can condition it on the observed metric data (b) in order to obtain a posterior distribution. Finally, we use this posterior distribution along with additional statistics obtained from the data (such as for example the best metric value attained so far) in order to compute a acquisition function \(a(\mathbf{x})\), an (approximate) maximum of which will be our suggested configuration. While \(a(\mathbf{x})\) can itself be difficult to globally optimize, it is available in closed form and can typically be differentiated w.r.t. \(\mathbf{x}\). Moreover, it is important to understand that \(a(\mathbf{x})\) is not an approximation to \(f(\mathbf{x})\), but instead scores the expected value of sampling the objective at \(\mathbf{x}\), thereby embodying the explore-exploit trade-off. In particular, once some \(\mathbf{x}_*\) is chosen and included into the set (a), \(a(\mathbf{x}_*)\) is much diminished.

The Bayesian optimization template requires us to make two choices:

  • Surrogate model: By far the most common choice is to use Gaussian process surrogate models (the tutorials linked above explain the basics of Gaussian processes). A Gaussian process is parameterized by a mean and a covariance (or kernel) function. In Syne Tune, the default corresponds to what is most frequently used in practice: Matern 5/2 kernel with automatic relevance determination (ARD). A nice side effect of this choice is that the model can learn about the relative relevance of each hyperparameter as more metric data is obtained, which allows this form of Bayesian optimization to render the curse of dimensionality much less severe than it is for random search.

  • Acquisition function: The default choice in Syne Tune corresponds to the most popular choice in practice: expected improvement.

GP-based Bayesian optimization is run by our launcher script with the argument --method BO. Many options can be specified via search_options, but we use the defaults here. See GPFIFOSearcher for all details. In our example, we set num_init_random to n_workers + 2, which is the number of initial decisions made by random search, before switching over to maximizing the acquisition function.

Results for Bayesian Optimization

Results for Bayesian Optimization

Results for Bayesian Optimization

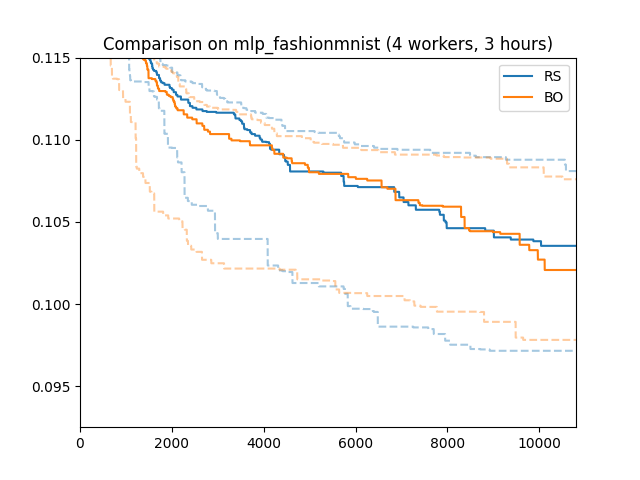
Here is how Bayesian optimization performs on our running example, compared to random search. We used the same conditions (4 workers, 3 hours experiment time, 50 random repetitions).

In this particular setup, Bayesian optimization does not outperform random search after 3 hours. This is a rather common pattern. Bayesian optimization requires a certain amount of data in order to learn enough about the objective function (in particular, about which parameters are most relevant) in order to outperform random search by targeted exploration and exploitation. If we continued to 4 or 5 hours, we would see a significant difference.

Recommendations

Here, we collect some additional recommendations. Further details are found here.

Categorical Hyperparameters

While our running example does not have any, hyperparameters of categorical type are often used. For example:

from syne_tune.config_space import lograndint, choice

config_space = {
    'n_units_1': lograndint(4, 1024),
    # ...
    'activation': choice(['ReLU', 'LeakyReLU', 'Softplus']),
}

Here, activation could determine the type of activation function. It is important to understand that in Bayesian optimization, a categorical parameter is encoded as vector in the multi-dimensional unit cube: the encoding dimension is equal to the number of different values. This is to make sure there is no ordering information between the different values, each pair has the same distance in the encoding space.

This is usually not what you want with numerical values, whose ordering provide important information to the search. For example, it sounds simpler to search over the finite range choice([4, 8, 16, 32, 64, 128, 256, 512, 1024]) than over the infinite lograndint(4, 1024) for n_units_1, but the opposite is the case. The former occupies 9 dimensions, the latter 1 dimension in the encoded space, and ordering information is lost for the former. A better alternative is logfinrange(4, 1024, 9).

Syne Tune provides a range of finite numerical domains in order to avoid suboptimal performance of Bayesian optimization due to the uncritical use of choice. Since this is somewhat subtle, and you may also want to import configuration spaces from other HPO libraries which do not have these types, Syne Tune provides an automatic conversion logic with streamline_config_space(). Details are given here.

Note

When using Bayesian optimization or any other model-based HPO method, we strongly recommend to use streamline_config_space() in order to ensure that your domains are chosen in a way that works best with internal encoding.

Speeding up Decision-Making

Gaussian process surrogate models have many crucial advantages over other probabilistic surrogate models typically used in machine learning. But they have one key disadvantage: inference computations scale cubically in the number of observations. For most HPO use cases, this is not a problem, since no more than a few hundred evaluations can be afforded.

Syne Tune allows to control the number of observations the GP surrogate model is fit to, via max_size_data_for_model in search_options. If the data is larger, it is downsampled to this size. Sampling is controlled by another argument max_size_top_fraction. Namely, this fraction of entries in the downsampled set are filled by those points in the full set with the best metric values, while the remaining entries are sampled (with replacement) from the rest of the full set. The default for max_size_data_for_model is DEFAULT_MAX_SIZE_DATA_FOR_MODEL. The feature is switched off by setting this to None or a very large value, but this is not recommended. Subsampling is repeated every time the surrogate model is fit.

Beyond, there are some search_options arguments you can use in order to speed up Bayesian optimization. The most expensive part of making a decision consists in refitting the parameters of the GP surrogate model, such as the ARD parameters of the kernel. While this refitting is essential for good performance with a small number of observations, it can be thinned out or even stopped when the dataset gets large. You can use opt_skip_init_length, opt_skip_period to this end (details are here.

Warping of Inputs

If you use input_warping=True in search_options, inputs are warped before being fed into the covariance function, the effective kernel becomes \(k(w(x), w(x'))\), where \(w(x)\) is a warping transform with two non-negative parameters per component. These parameters are learned along with other parameters of the surrogate model. Input warping allows the surrogate model to represent non-stationary functions, while still keeping the numbers of parameters small. Note that only such components of \(x\) are warped which belong to non-categorical hyperparameters.

Box-Cox Transformation of Target Values

This option is available only for positive target values. If you use boxcox_transform=True in search_options, target values are transformed before being fitted with a Gaussian marginal likelihood. This is using the Box-Cox transform with a parameter \(\lambda\), which is learned alongside other parameters of the surrogate model. The transform is \(\log y\) for \(\lambda = 0\), and \(y - 1\) for \(\lambda = 1\).

Both input warping and Box-Cox transform of target values are combined in this paper:

Cowen-Rivers, A. et.al.
HEBO: Pushing the Limits of Sample-efficient Hyper-parameter Optimisation
Journal of Artificial Intelligence Research 74 (2022), 1269-1349
ArXiV

However, they fit \(\lambda\) up front by maximizing the likelihood of the targets under a univariate Gaussian assumption for the latent \(z\), while we learn \(\lambda\) jointly with all other parameters.